FI simulation on a linear array with the USTB built-in Fresnel simulator

In this example we show how to use the built-in fresnel simulator in USTB to generate a Conventional Focused Imaging (single focal depth) dataset for a linear array and a linear scan and show how it can be beamformed with USTB.

This tutorial assumes familiarity with the contents of the 'CPWC simulation with the USTB built-in Fresnel simulator' tutorial. Please feel free to refer back to that for more details.

by Alfonso Rodriguez-Molares alfonso.r.molares@ntnu.no and Arun Asokan Nair anair8@jhu.edu 14.03.2017

Phantom
Probe
Pulse
Sequence generation
The Fresnel simulator
Beamformer

Close all previously opened plots.

close all;

Phantom

We start off defining an appropriate phantom structure to image. Our phantom here is simply a single point scatterer. USTB's implementation of phantom comes with a plot method to visualize the phantom for free!

pha=uff.phantom();
pha.sound_speed=1540;            % speed of sound [m/s]
pha.points=[0,  0, 40e-3, 1];    % point scatterer position [m]
fig_handle=pha.plot();

Probe

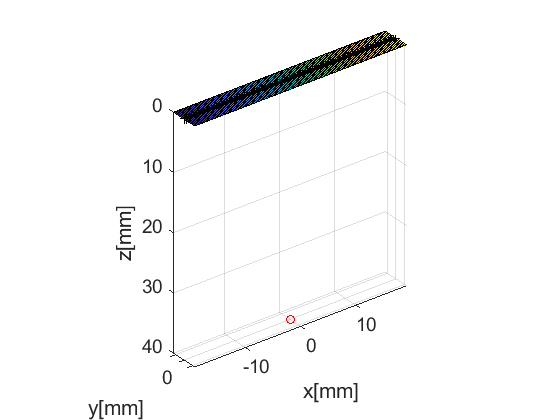
The next UFF structure we look at is probe. It contains information about the probe's geometry. USTB's implementation of probe comes with a plot method too. When combined with the previous figure we can see the position of the probe respect to the phantom.

prb=uff.linear_array();
prb.N=128;                  % number of elements
prb.pitch=300e-6;           % probe pitch in azimuth [m]
prb.element_width=270e-6;   % element width [m]
prb.element_height=5000e-6; % element height [m]
prb.plot(fig_handle);

Pulse

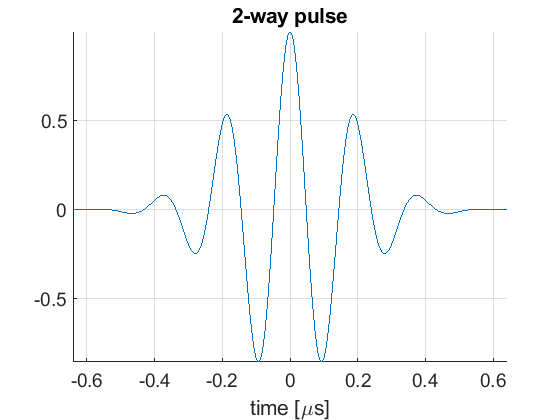
We then define the pulse-echo signal which is done here using the fresnel simulator's pulse structure. We could also use 'Field II' for a more accurate model.

pul=uff.pulse();
pul.center_frequency=5.2e6;       % transducer frequency [MHz]
pul.fractional_bandwidth=0.6;     % fractional bandwidth [unitless]
pul.plot([],'2-way pulse');

Sequence generation

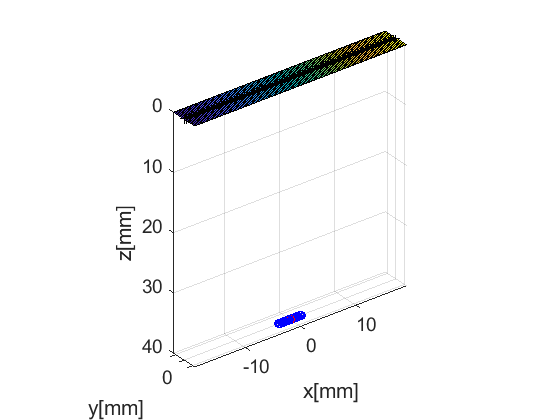
Now, we shall generate our sequence! Keep in mind that the fresnel simulator takes the same sequence definition as the USTB beamformer. In UFF and USTB a sequence is defined as a collection of wave structures.

For our example here, we define a sequence of 200 focused beams spanning a lateral range of $[-2, 2]$ mm. The focal depth is set as 40 mm. The wave structure too has a plot method.

N=50;                               % number of focused beams
x_axis=linspace(-2e-3,2e-3,N).';
z0=40e-3;
seq=uff.wave();
for n=1:N
    seq(n)=uff.wave();
    seq(n).probe=prb;

    seq(n).source.xyz=[x_axis(n) 0 z0];

    seq(n).apodization=uff.apodization();
    seq(n).apodization.window=uff.window.tukey50;
    seq(n).apodization.f_number=1.7;
    seq(n).apodization.focus=uff.scan('xyz',seq(n).source.xyz);

    seq(n).sound_speed=pha.sound_speed;

    % show source
    fig_handle=seq(n).source.plot(fig_handle);
end

The Fresnel simulator

Finally, we launch the built-in simulator. The simulator takes in a phantom, pulse, probe and a sequence of wave structures along with the desired sampling frequency, and returns a channel_data UFF structure.

sim=fresnel();

% setting input data
sim.phantom=pha;                % phantom
sim.pulse=pul;                  % transmitted pulse
sim.probe=prb;                  % probe
sim.sequence=seq;               % beam sequence
sim.sampling_frequency=41.6e6;  % sampling frequency [Hz]

% we launch the simulation
channel_data=sim.go();

USTB's Fresnel impulse response simulator (v1.0.7)
---------------------------------------------------------------

Beamformer

With channel_data and a scan we have all we need to produce an ultrasound image. We now use a USTB structure midprocess, that takes an apodization structure in addition to the channel_data and scan.

midproc=midprocess.das();
midproc.dimension = dimension.both;
midproc.channel_data=channel_data;
midproc.scan=uff.linear_scan('x_axis',x_axis,'z_axis',linspace(39e-3,41e-3,100).');

midproc.transmit_apodization.window=uff.window.scanline;
midproc.receive_apodization.window=uff.window.tukey50;
midproc.receive_apodization.f_number=1.7;

b_data=midproc.go();
b_data.plot([],'No MLA');

USTB General beamformer MEX v1.1.2 .............done!

The image is ok, but we can use multiline acquisition (MLA) to improve resolution. We choose to use MLA = 4 and we define a new scan where we increase the number of scan lines by a factor of 4. We also need to tell the apodization function that we will use MLA = 4 scheme.

MLA = 4;
midproc.scan=uff.linear_scan('x_axis',linspace(-2e-3,2e-3,MLA*N).','z_axis',linspace(39e-3,41e-3,100).');
midproc.transmit_apodization.MLA = MLA;
midproc.transmit_apodization.MLA_overlap = 0;
b_data=midproc.go();
b_data.plot([],'MLA=4, no overlap');

USTB General beamformer MEX v1.1.2 .............done!

Mmmm... Somewhat better. But we see a strange artifact between each MLA group. We can mitigate this effect introducing some MLA overlap

midproc.transmit_apodization.MLA_overlap = 2;
b_data=midproc.go();
b_data.plot([],'MLA=4, overlap=2');

uff.apodization: Inputs and outputs are unchanged. Skipping process.
USTB General beamformer MEX v1.1.2 .............done!