DW simulation with a linear array using the USTB built-in Fresnel simulator

In this example, we show how to use the built-in Fresnel simulator in USTB to generate a Diverging Wave (DW) dataset on a linear array, and then beamform it with USTB.

This tutorial assumes familiarity with the contents of the 'CPWC simulation with the USTB built-in Fresnel simulator' tutorial. Please feel free to refer back to that for more details.

by Alfonso Rodriguez-Molares alfonso.r.molares@ntnu.no and Arun Asokan Nair anair8@jhu.edu 23.02.2017

Contents

Phantom

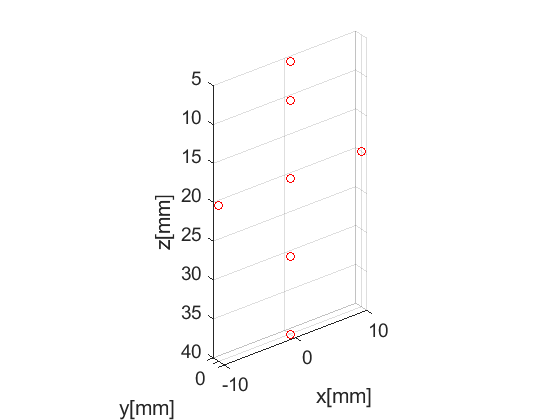
First step - define our phantom. Here, our phantom is a single point scatterer. USTB's implementation of phantom comes with a plot method for free!

pha=uff.phantom();
pha.sound_speed=1540;                 % speed of sound [m/s]
pha.points=[0,  0,  5e-3, 1;...
            0,  0, 10e-3, 1;...
            0,  0, 20e-3, 1;...
            0,  0, 30e-3, 1;...
            0,  0, 40e-3, 1;...
             10e-3,  0, 20e-3, 1;...
            -10e-3,  0, 20e-3, 1];    % point scatterer position [m]
fig_handle=pha.plot();

Probe

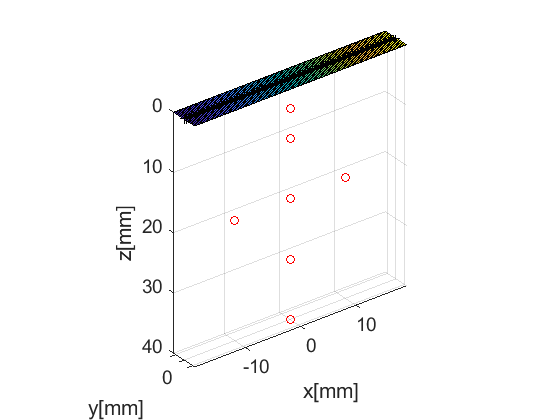
The next step is to define the probe structure which contains information about the probe's geometry. This too comes with a plot method that enables visualization of the probe with respect to the phantom. The probe we will use in our example is a linear array transducer with 128 elements.

prb=uff.linear_array();
prb.N=128;                  % number of elements
prb.pitch=300e-6;           % probe pitch in azimuth [m]
prb.element_width=270e-6;   % element width [m]
prb.element_height=5000e-6; % element height [m]
prb.plot(fig_handle);

Pulse

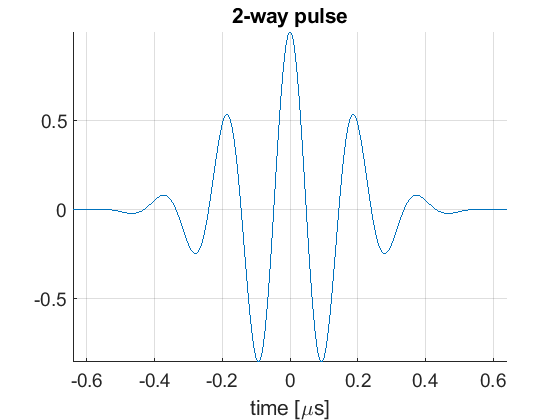
We then define the pulse-echo signal which is done here using the fresnel simulator's pulse structure. We could also use 'Field II' for a more accurate model.

pul=uff.pulse();
pul.center_frequency=5.2e6;       % transducer frequency [MHz]
pul.fractional_bandwidth=0.6;     % fractional bandwidth [unitless]
pul.plot([],'2-way pulse');

Sequence generation

Now, we shall generate our sequence! Keep in mind that the fresnel simulator takes the same sequence definition as the USTB beamformer. In UFF and USTB a sequence is defined as a collection of wave structures.

For our example here, we define a sequence of 31 diverging waves. The wave structure has a plot method which plots the direction of the transmitted waves.

N=31;                      % number of diverging waves
x0=linspace(-19.2e-3,19.2e-3,N);
z0=-20e-3;
seq=uff.wave();
for n=1:N
    seq(n)=uff.wave();
    seq(n).probe=prb;
    seq(n).source.xyz=[x0(n) 0 z0];
    seq(n).sound_speed=pha.sound_speed;

    % show source
    fig_handle=seq(n).source.plot(fig_handle);
end

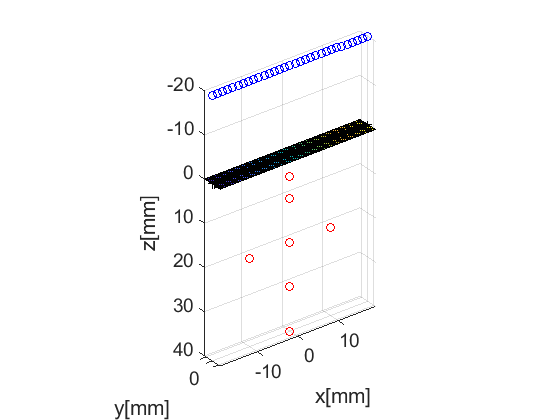
The Fresnel simulator

Finally, we launch the built-in simulator. The simulator takes in a phantom, pulse, probe and a sequence of wave structures along with the desired sampling frequency, and returns a channel_data UFF structure.

sim=fresnel();

% setting input data
sim.phantom=pha;                % phantom
sim.pulse=pul;                  % transmitted pulse
sim.probe=prb;                  % probe
sim.sequence=seq;               % beam sequence
sim.sampling_frequency=41.6e6;  % sampling frequency [Hz]

% we launch the simulation
channel_data=sim.go();

USTB's Fresnel impulse response simulator (v1.0.7)
---------------------------------------------------------------

Scan

The scan area is defines as a collection of pixels spanning our region of interest. For our example here, we use the linear_scan structure, which is defined with two axes - the lateral axis and the depth axis. scan too has a useful plot method it can call.

scan=uff.linear_scan('x_axis', linspace(-19.2e-3,19.2e-3,200).', 'z_axis', linspace(0e-3,45e-3,100).');
scan.plot(fig_handle,'Scenario');    % show mesh

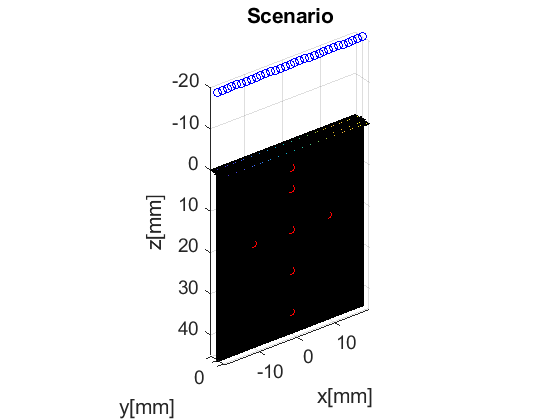
Midprocessor

With channel_data and a scan we have all we need to produce an ultrasound image. We now use a USTB structure pipeline, that takes an apodization structure in addition to the channel_data and scan.

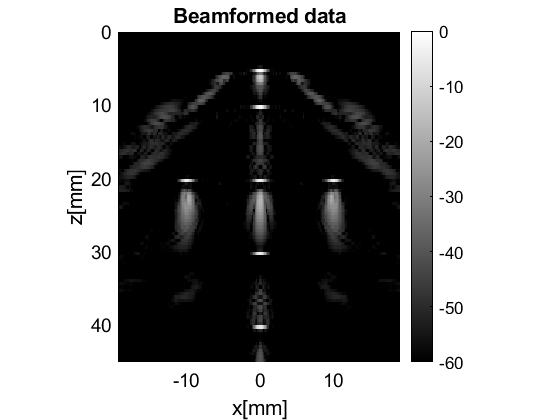
mid=midprocess.das();
mid.dimension = dimension.both;
mid.channel_data=channel_data;
mid.scan=scan;

F_number=1.7;
mid.receive_apodization.window=uff.window.hanning;
mid.receive_apodization.f_number=F_number;
mid.receive_apodization.minimum_aperture = [3e-3 3e-3];

mid.transmit_apodization.window=uff.window.hanning;
mid.transmit_apodization.f_number=F_number;
mid.transmit_apodization.minimum_aperture = [3e-3 3e-3];

b_data=mid.go();
b_data.plot();

USTB General beamformer MEX v1.1.2 .............done!

Published with MATLAB® R2020b